Top 10 Toughest Class 12 Maths Problems and Expert Tips to Crack Them

Mastering Class 12 Math is one of the biggest academic milestones for students aiming for top scores in board exams and entrance tests like JEE Main, JEE Advanced, BITSAT, etc.. While solving basic textbook problems might seem manageable, the real challenge begins when you’re faced with advanced, tricky, and conceptual problems that truly test your skills.

If you’re wondering how to tackle the most difficult questions from chapters like Integration, 3D Geometry, Probability, and Differential Equations, you’re in the right place.

In this blog, we have handpicked the 10 most challenging Class 12 Maths problems, along with proven expert tips and strategies to help you solve them step-by-step.

Whether you’re a CBSE, ISC, or international curriculum student, these insights will give you the edge you need to excel.

Why Some Class 12 Math Problems Are Tough?

Before diving in, it’s important to know why certain problems are more difficult:

• They involve multiple concepts from different chapters.
• They test your logical reasoning, not just formulas.
• They include tricky traps—easy to fall into if you’re rushing.
• They require advanced algebraic manipulation or visualization.

If you’re aiming for top scores or preparing for exams like JEE Main/Advanced, CBSE, ISC, or IB, this list will help you stay ahead.

Top 10 Most Challenging Class 12 Maths Problems + Tips to solve them

Problem 1: Integration by Parts with Logarithms

Evaluate :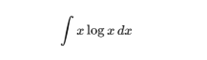

Why it’s hard:

It’s not straightforward and requires using integration by parts, which many students misuse.

Tip to Solve:

Use

Let The correct choice of u is critical here.

Problem 2: Tangents and Normals

Find the equation of the normal to the curve

y = x³−3x+2 at the point where the tangent is horizontal.

Why it’s hard:

You have to differentiate, find where the slope is zero, and then plug that into the normal formula.

Tip to Solve:

• Differentiate to get dy/dx
• Set dy/dx=0 to find the x-value of horizontal tangent
• Use the point-slope form of a line to find the normal

Problem 3: 3D Geometry—Distance Between Skew Lines

Find the shortest distance between the lines

Why it’s hard:

You need to understand vector operations and geometric intuition—many students confuse parallel with skew lines.

Tip to Solve:

Use the formula:

Problem 4: Continuity and Differentiability

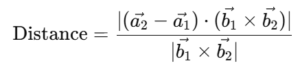
Determine the value of 𝑘 for which the function

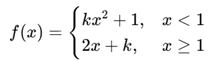
is continuous and differentiable at x=1.

Why it’s hard:

You must match both the function values and derivatives from either side—a classic board trap.

Tip to Solve: 

• Ensure
• Match derivatives on both sides at x=1

Problem 5: Bayes’ Theorem in Probability

A factory has 3 machines producing bulbs. Machine A produces 30% of total, B 45%, and C 25%. The probability of producing a defective bulb is 1% for A, 2% for B, and 3% for C. A bulb is chosen at random and found defective. What is the probability it came from Machine B?

Why it’s hard:

Students struggle with Bayes’ Theorem, especially with conditional probability.

Tip to Solve:

Use:

Break it down step by step and use a probability tree if needed.

Problem 6: Complex Numbers Geometry

Prove that the triangle with vertices represented by complex numbers

Why it’s hard:

You must visualize complex numbers as vectors and use modulus as length.

Tip to Solve:

Calculate the modulus of sides (i.e., distances between points) using

Compare them to prove two are equal.

Problem 7: Linear Programming Graphical Method

Maximize Z=3x+5y subject to

Why it’s hard:

Plotting inequalities and identifying feasible regions is time-consuming and error-prone.

Tip to Solve:

Graph each inequality clearly

Mark the feasible region

Evaluate the objective function at each vertex

Problem 8: Differential Equations Form

Solve:

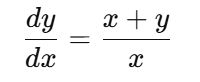
Why it’s hard:

It’s a first-order linear differential equation that requires smart substitution.

Tip to Solve:

Let

Substitute and simplify to solve.

Problem 9: Determinants—Properties

Evaluate

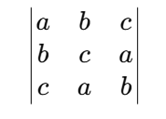
Why it’s hard:

Needs application of determinant properties (row/column operations).

Tip to Solve:

Try adding or subtracting rows/columns to simplify—symmetry can often help.

Problem 10: Application of Derivatives

Find the maximum area of a rectangle inscribed in a semicircle of radius 𝑟.

Why it’s hard:

Involves a combination of geometry, trigonometry, and calculus.

Tip to Solve:

Express area in terms of one variable using Pythagoras

Differentiate and find the maximum

General Tips to Tackle Challenging Class 12 Maths Problems

• Master the basics first. Make sure your fundamentals are strong before jumping into tough problems.
• Visualize the question. Sketch graphs, draw vectors, or make a probability tree to better understand the problem.
• Break the question into steps. Don’t try to solve everything at once—modular thinking is key.
• Practice daily. Consistency matters more than cramming.
• Review your mistakes. Every tough problem you fail to solve is a chance to learn faster.

Chapter-Wise Strategy for Class 12 Maths Success

Before diving into the toughest problems, let’s get a bird’s-eye view of how to approach each important chapter. Here are quick strategies to tackle them smartly:

Chapter	Smart Strategy
Relations & Functions	Understand domain/range visually; use mapping diagrams
Inverse Trigonometry	Memorize principal values and identity transformations
Matrices & Determinants	Practice row/column operations; use shortcuts for large matrices
Continuity & Differentiability	Focus on left-hand/right-hand limits and derivative matching
Applications of Derivatives	Know how to identify max/min points; practice geometry-based problems
Integrals	Master substitution, parts, and partial fractions separately
Differential Equations	Learn standard forms; practice solving homogeneous cases
Vector Algebra & 3D Geometry	Visualize direction ratios and vector cross products
Linear Programming	Learn to graph inequalities and spot feasible regions fast
Probability	Use Venn diagrams and tree diagrams to simplify problems

This table will help you revise and prioritize what to focus on in each topic before taking on advanced-level problems.

Weekly Study Plan: Boards + JEE (or Other Entrance Exams)

Managing both board-level preparation and competitive exams can be overwhelming. Here’s a sample weekly routine to balance both effectively:

Day	Focus Area
Monday	Board-level problem practice (NCERT)
Tuesday	JEE/Advanced-level problems
Wednesday	Exemplar/CBSE sample papers
Thursday	Focus on weak chapters (concepts + practice)
Friday	Mixed problem-solving + revision
Saturday	Full mock test (alternate weeks)
Sunday	Error log analysis + light revision

📌 Tip: Use a timer when solving problems to improve speed and accuracy. Over time, this routine builds both confidence and consistency.

Common Mistakes to Avoid

• Plugging values too early before simplifying
• Forgetting to check domain/restrictions
• Ignoring special conditions (like continuity or differentiability)
• Not revising NCERT and exemplar problems

Challenging problems aren’t just about toughness—they’re opportunities to sharpen your mind and build real confidence. Whether you’re targeting board exams or engineering entrances like JEE, mastering these problems will give you an edge.

So bookmark this blog, revisit one problem a day, and you’ll notice the difference in your problem-solving speed and accuracy!